Los
principios fundamentales de la cristalografía
morfológica, de los elementos de simetría y su
combinación para generar objetos repetitivos en el espacio,
fueron establecidos entre los siglos XVII y XIX, tal como se
recoge
en otro apartado de estas páginas...
Concretándonos
a los objetos finitos, existen varias operaciones (elementos
de simetría) que describen las repeticiones. En
las grecas nos encontramos con operaciones
de traslación (el motivo se repite por
traslación). La repetición de los
pétalos de las flores nos conduce a operaciones de giro (el
motivo se repite por giro) alrededor de ejes
de simetría (o ejes
de rotación). Y, aunque no exactamente, la
simetría que nos muestra la partitura o la frase sobre el
Abad nos llevaría a considerar las operaciones denominadas planos
de simetría (o planos
de reflexión, es decir, la operación
que
ocurre
cuando uno se mira en un espejo). Análogamente, por ejemplo,
si nos fijamos en la relación entre los objetos
tridimensionales de alguna figura de más abajo,
descubriremos
también un
nuevo elemento de simetría denominado centro
de simetría (o centro
de inversión), que sería un punto
imaginario colocado entre ambos objetos.
En general, y si tenemos en cuenta que las traslaciones puras no se
consideran estrictamente como elementos de simetría, podemos
decir
que los objetos finitos pueden contener
en sí mismos, o pueden repetirse (excluyendo la
traslación), mediante los siguientes
elementos de simetría:
- La identidad,
que es la operación más simple de todas.
¡No hace nada!, pero es muy importante ya que cualquier
objeto
tiene, al menos, este elemento de simetría. Hay muchos
objetos
que sólo tienen este elemento de simetría.
- La reflexión
es la operación de simetría que
ocurre cuando colocamos un objeto frente a un espejo. La imagen que se
forma lo hace sobre la perpendicular al plano de reflexión
(el
espejo) y está equidistante de dicho plano, al otro lado del
mismo. El objeto resultante puede resultar distinguible o indistinguible
respecto del original, aunque normalmente resulta distinguible,
porque no puede
superponerse con aquel. Si el objeto original y su imagen resultan indistinguibles es
porque el plano de reflexión pasa por el interior del objeto.
- La inversión,
que ocurre a través de un punto único en el
espacio,
denominado centro de inversión. Cada parte del objeto se
mueve a
lo largo de una línea recta, que pasa por el centro de
inversión, hasta alcanzar la misma distancia que lo separa
de
dicho punto. El
objeto resultante puede resultar distinguible
o indistinguible
respecto del original, aunque normalmente resulta distinguible,
porque no puede
superponerse con aquel. Si el objeto original y su resultante son
indistinguibles
es porque el centro de inversión está en el
interior del objeto.
- Las operaciones de rotación
(las llamadas propias e impropias) son giros que ocurren alrededor de
una línea denominada eje de rotación. a)
Una
rotación propia
es aquella que ocurre girando 360°/n, en donde n es el llamado
orden del eje. El objeto resultante tras el giro es siempre indistinguible del
original. b)
Una rotación impropia
se realiza por giro de 360°/n seguida de una
reflexión a través de un plano perpendicular al
eje de rotación. El objeto resultante puede resultar distinguible o indistinguible
respecto del original, aunque normalmente resulta distinguible,
porque no puede
superponerse con aquel. Si el objeto original y su resultante son
indistinguibles
es porque el eje de
rotación impropia pasa por el interior del objeto.
Además del nombre con
el que designamos los elementos de simetría, en
cristalografía se usan símbolos
(gráficos y numéricos) que los representan.
Por ejemplo, un eje de rotación de orden 2 (eje binario), se
representa por el número 2,
y un plano de reflexión se representa mediante la letra m.
Manos (izquierda y derecha) relacionadas
por un centro de simetría
Objetos
circulares relacionados por un centro de simetría, y poliedro
que muestra únicamente un centro de simetría en
su punto
medio
La asociación de
elementos de
rotación con centros o planos de simetría genera
nuevos
elementos de simetría denominados rotaciones
impropias.
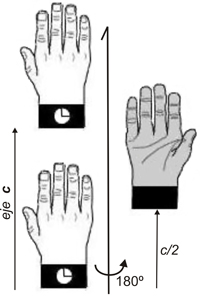
Izquierda:
Un
eje de rotación cuaternario implica rotaciones de
90º
seguidas de reflexiones a través de un plano de
simetría
perpendicular al mencionado eje. Animacón
tomada de M.
Kastner, T. Medlock & K. Brown, Univ. of Bucknell)
Derecha: Eje
de rotación impropia, vertical, en un modelo de cristal como
el de
urea.
El significado de los tripletes numéricos mostrados
será
descutido en otro capítulo.
Combinando
los elementos de simetría del tipo ejes de
rotación y planos de
reflexión, con las
traslaciones
características
de un cristal (que veremos más abajo), surgen nuevos
elementos
de
simetría con componentes de deslizamiento (ejes
helicoidales
y planos
de deslizamiento).
Los
elementos de
simetría
del tipo centro
y plano,
relacionan de un modo peculiar los motivos que repiten, el mismo modo
que
relaciona entre sí nuestras manos, que no son superponibles.
Los
motivos que no contienen en sí mismos ninguno de estos
elementos
de simetría (centro o plano) se denominan quirales
y
su repetición mediante estos elementos de
simetría
(centro
o plano) genera objetos que se denominan
enantiómeros
respecto
de los originales (la imagen especular de una de nuestras
manos
es enantiómera de la que ponemos delante del espejo). En
relación con la quiralidad de los cristales y de
las
unidades (moleculares o no) que los forman, el lector avanzado
debería leer también el artículo
de Howard D. Flack que podrá encontrar a través
de este enlace.
La
imagen especular de cualquiera de nuestras manos es el
enantiómero
de la otra mano. Son objetos no superponibles y al no contener en
sí
mismas ni centros ni planos de simetría se denominan objetos
quirales.
Las moléculas quirales tienen
propiedades diferentes de sus
enantiómeras y su diferenciación es importante.
La
determinación correcta de la estructura
ó
configuración absoluta de una
molécula (diferenciación
entre enantiómeros)
puede realizarse de un modo seguro exclusivamente mediante la
difracción de rayos X, pero eso será objeto de otro
apartado que
trataremos más
adelante.
Asi pues, cualquier objeto finito (como un cristal de
cuarzo, una
silla, o una flor) muestra determinadas partes de él que se
repiten mediante operaciones de simetría, y éstas
pasan
por un punto del objeto, formando lo que se denomina
grupo
puntual de simetría del objeto. El lector
avanzado tiene la posibilidad de consultar
también estas las magníficas ayudas sobre grupos
puntuales, o en general sobre simetría, que se ofrecen a
través de estos enlaces:
Adicionalmente, el lector puede descargar y ejecutar en su propio
computador
esta
aplicación Java que como introducción a la
simetría de los poliedros que desarrollaron
Gervais
Chapuis y Nicolas Schöni (École Polytechnique
Fédérale de Lausanne, Suiza).
Simetría en los cristales
En los cristales,
los ejes
de simetría
(ejes de rotación)
sólo pueden ser
binarios
(2),
ternarios
(3),
cuaternarios
(4)
ó senarios
(6),
dependiendo del número de repeticiones que se produzcan del
motivo (orden
de la rotación).
Así, un eje de
orden 3 (ternario) produce 3
repeticiones del motivo, una cada 360/3=120
grados de giro. Si algún lector se pregunta por
qué
sólo se mencionan ejes de orden 2,
3,
4
y 6,
y por qué no
los de orden 5,
7,
etc., le recomendamos que consulte las explicaciones
que se dan en otro
apartado.
Las
rotaciones
impropias
(rotaciones seguidas de reflexión a
través de un
plano perpendicular al eje de giro) se designan con el
número del
orden de
la rotación, con una barra encima del número.
Los ejes
helicoidales (ejes
de simetría que implican giro y traslación a lo
largo de un
eje de traslación) se representan con el número
de orden de la
rotación, con
un subíndice añadido que cuantifica el
deslizamiento a lo
largo del eje. Así, un eje helicoidal del tipo representa
que en cada una de las 6
rotaciones, la traslación asociada es de 2/6
de la periodicidad en la dirección del eje de la celdilla
elemental.
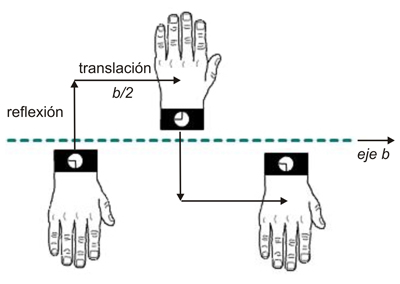
Los planos
de simetría (espejos) se representan por la
letra m.
Los planos
de deslizamiento
(planos de simetría que implican reflexión
seguida de
traslación paralela al plano) se representan por las letras a,
b,
c,
n
ó d,
dependiendo de que la traslación asociada a la
reflexión sea paralela a las traslaciones reticulares (a,
b,
c)
o a una diagonal de un plano reticular (n)
ó a una diagonal de la celdilla elemental (d).
Las letras o números que representan a los elementos de
simetría tienen también una equivalencia con
determinados
símbolos
gráficos.
Pero para
poder seguir
hablando
de la simetría en los cristales, es necesario introducir y
recordar el aspecto fundamental que los define, que es la
repetición periódica por traslación de
motivos (átomos, moléculas o iones). Esta
repetición, que se ilustra en dos dimensiones con
círculos grises de la figura de abajo, se deriva del
concepto matemático de red que veremos con mayor propiedad
en otro
capítulo.
La repetición
periódica por la que se describe la
estructura interna de los cristales viene representada por un conjunto
de traslaciones en las tres direcciones del espacio, de tal forma que
el cristal puede considerarse como un apilamiento, en tres dimensiones,
de bloques idénticos. Cada bloque, de una forma y
tamaño
determinados (pero todos iguales), se denomina celdilla
unidad ó celdilla
elemental. Su tamaño viene
determinado por la
longitud de sus tres aristas (a,
b,
c),
y la forma por el valor de los ángulos entre dichas aristas
(alpha, beta, gamma: α, β, γ).
Apilamiento
de celdillas formando un cristal con
morfología octaédrica, y parámetros
(ejes y ángulos) que caracterizan la forma y
tamaño de una celdilla elemental
(ó
celdilla unidad)
Tal como hemos dicho
más arriba, el conjunto de
elementos de simetría de un objeto finito, que pasan por un
punto, definen la simetría total del objeto y se denominan
grupo
puntual de simetría.
Obviamente, los elementos de simetría que implican
traslaciones
de tipo reticular (planos de deslizamiento y ejes helicoidales), no
forman parte de las operaciones de simetría de los grupos
puntuales.
Grupos
puntuales hay muchos, pero en los cristales han de ser
compatibles con la periodicidad (repetitividad por
traslación) que los describe internamente. Así,
en los cristales sólo son posibles las rotaciones
(ejes
de simetría)
de orden 2, 3, 4 y 6, es decir, las repeticiones mediante giros de
180º (=360/2), 120º (=360/3), 90º (=360/4) y
60º
(=360/6). Véase también el teorema
de restriccción cristalográfica. Con
todo ello,
en los cristales nos encontramos con sólo 32
grupos puntuales posibles,
que se denominan clases
cristalinas.
grupo puntual . periodicidad por
traslación del cristal = 32 clases cristalinas
El motivo, constituído por un
simple ladrillo, puede
representarse
por un punto reticular y contiene la simetría
puntual 2mm
En las tres tablas siguientes se muestran visualizaciones animadas para
cada una de las 32 clases cristalinas, agrupadas en que se denominan sistemas
cristalinos
(columna de la izquierda), y que simplemente son un modo de
clasificación en términos de simetría
mínima, tal como se verá más abajo.
Lluis Casas y Eugenia Estop,
desde el
Departamento de Geología de la Universidad de
Barcelona, ofrecen 32
ficheros pdf
que, de un modo interactivo, permiten familiarizarse con los 32 grupos
puntuales a través de la simetría de
sólidos
cristalinos.
Adicionalmente, el lector puede
descargar (totalmente libre de virus) y
ejecutar en su propio
computador esta
aplicación Java que como introducción a la
simetría de los poliedros desarrollaron Gervais
Chapuis y Nicolas Schöni (École Polytechnique
Fédérale de Lausanne, Suiza).
Alternativamente el lector interesado puede visualizar en modo
interactivo algunos poliedros típicos de los 7 sistemas
cristalográficos , a través del Instituto
Gemológico Español.
De las 32
clases
cristalinas, sólo 11
contienen al operador centro
de simetría y a éstas clases
cristalinas centrosimétricas se les conoce con
el nombre de
grupos
de Laue.
clase
cristalina . centro
de simetría = 11
grupos de
Laue
A
su vez, en los cristales, las formas de repetición por
traslación
tienen que ser compatibles con la simetría puntual (las 32
clases
cristalinas), de modo que sólo nos encontramos con 14
tipos de redes de traslación que son
compatibles con
las clases cristalinas. A estos tipos de redes (modos de
repetición
por traslación) de los cristales se les llama
también redes
de Bravais (las
puedes
ver aqui). La
simetría traslacional de
una
distribución
ordenada de objetos en 3 dimensiones se puede describir mediante muchos
tipos de redes, pero hay una que se adecúa más al
objeto,
es decir, que describe mejor, a la vez, la simetría propia
del
objeto.
Y es que, como las redes a su vez tienen su propia
distribución
de elementos de simetría, hay que adecuar éstos a
los de
la estructura.
periodicidad
traslacional del
cristal . 32 clases
cristalinas = 14 redes de
Bravais
representación
gráfica de las redes de Bravais
Una
pared de ladrillos puede estructurarse con diferentes tipos de redes,
pasando
por diferentes orígenes, definiendo puntos reticulares que
representan
todo el ladrillo. Pero hay una que es más adecuada a la
simetría
del ladrillo y a la disposición de éstos al
formar la
pared.
La
adecuación de
una red a una estructura se muestra en los ejemplos
bidimensionales
inferiores, en donde en los tres casos hay dos redes, una primitiva
oblícua
y otra rectangular centrada. En los dos primeros casos, la red
rectangular resulta la
más adecuada, mientras que
la deformación de la estructura alcanza, en el tercer
ejemplo, unas relaciones métricas que hacen que la red
más adecuada sea la primitiva oblícua, hexagonal
en
este caso.
Adecuación
del tipo de red a la estructura. La red azul
es la más adecuada en cada caso
Por último, al combinar los grupos puntuales de
los
cristales (las
32
clases cristalinas) con las
14
redes de Bravais, nos encontramos con
230
maneras posibles
de repetir un objeto finito (motivo)
en el espacio de 3 dimensiones. A estos 230 modos de
repetición de motivos en el espacio, que son compatibles con
las clases cristalinas y con las redes de Bravais, se les denomina
grupos
espaciales, que representan las diferentes formas de
adecuar la redes de Bravais con la simetría de las
estructuras. El lector interesado debería consultar
también
el
magnífico trabajo que, sobre los elementos de
simetría
presentes en los grupos espaciales, ofrecen Margaret Kastner, Timathy
Medlock y Kristy Brown a través de este enlace de la
Universidad
de Bucknell.
32
clases cristalinas
+ 14 redes de Bravais
= 230 Grupos
Espaciales
Representación
de la red de la pared de ladrillos, más acorde con el motivo
(ladrillo)
y sus elementos de simetría. Nótese que, en este
caso, la
simetría puntual del ladrillo y la puntual del nudo de red
coinciden.
El grupo espacial (si consideramos el espesor del ladrillo) es
Cmm2.
Estas 32 clases, 14 redes
y 230 grupos espaciales pueden clasificarse, según la
simetría mínima que albergan, en 7
sistemas cristalinos.
La simetría mínima produce restricciones en los
valores
métricos
(distancias y ángulos) que describen la forma y el
tamaño
de la red.
32 clases, 14 redes, 230
grupos espaciales
/ simetría cristalina
= 7 sistemas
cristalinos
Todo ello se resume
en
el siguiente esquema:
Clases
cristalinas
(* clases de Laue) |
Redes
cristalinas compatibles
y su
simetría |
Número
de
grupos espaciales |
Simetría
mínima |
Restricción
métrica |
Sistema
cristalino |
| 1
1 * |
P
1 |
2 |
1
ó
1 |
ninguna |
Triclínico |
| 2
m
2/m * |
P
C (I)
2/m |
13 |
Un 2
ó
2 |
α=γ=90
|
Monoclínico |
| 222
2mm
mmm * |
P
C (A,B) I
F
mmm |
59 |
Tres
2
ó 2 |
α=β=γ=90
|
Ortorrómbico |
4
4 4/m *
422 4mm
42m
4/mmm * |
P
I
4/mmm |
68 |
Un
4
ó 4 |
a=b
α=β=γ=90
|
Tetragonal |
3
3
*
32 3m 3m
* |
P
(R)
3m
6/mmm |
25 |
Un
3
ó 3 |
a=b=c
α=β=γ
(ó
Hexagonal)
|
Trigonal |
6
6
6m *
622 6mm
6m2
6/mmm * |
P
6/mmm |
27 |
Un
6
ó 6 |
a=b
α=β=90
γ=120 |
Hexagonal |
23
m3 *
432 43m
m3m * |
P
I
F
m3m |
36 |
Cuatro 3
ó 3 |
a=b=c
α=β=γ=90
|
Cúbico |
Total:
32, 11 *
|
14
independientes |
230 |
|
|
7 |
Los
230 grupos espaciales
vienen recogidos y descritos en las International
Tables for X-ray Crystallography,
en donde se
encuentran
clasificados
según los grupos puntuales y los sistemas cristalinos. Los
compuestos quirales que se preparan como un único
enantiómero (por ejemplo, las moléculas
biológicas) pueden cristalizar solamente en un subconjunto
de 65
grupos espaciales, aquellos que no tienen operaciones de
simetría del tipo plano de simetría (es decir,
espejo)
y/o centro de inversión.
Un
ejemplo
de parte de la información contenida en estas Tablas se
muestra
a continuación para el grupo espacial Cmm2,
en el que la C
significa que la
estructura
se describe con una red centrada en las caras separadas por el eje c,
la primera m
representa un plano
de
simetría perpendicular al eje a,
la segunda al eje b,
y el 2
se refiere al eje binario paralelo al eje c.
Resumen
de la información existente en International
Tables for X-ray Crystallography para
el grupo espacial Cmm2
Resumen
de la información existente en The
International
Tables for X-ray Crystallography para
el grupo espacial P21/c
El lector avanzado puede, además, consultar:
¡Un
cristalógrafo nunca se aburre! Trata de disfrutar de todo
esto buscando la simetría de los objetos que se encuentran a
tu alrededor y en particular en estos ejemplos de más
abajo...
(las soluciones se obtienen pinchando en cada imagen)
Busque posibles celdillas
y elementos de simetría en esta
felicitación de Año Nuevo 2022
(la solución se obtiene pinchando en la imagen)
Busque posibles celdillas
y elementos de simetría en esta
felicitación de Año Nuevo 2023
(la solución se obtiene pinchando en la imagen)
Hay una pregunta que
con toda seguridad los lectores se habrán planteado, y es
que en
este capítulo hemos hablado de la existencia de elementos de
simetría que operan en el interior de los cristales, pero
aun no hemos dicho cómo podemos averiguar la existencia de
dichas
operaciones, cuando en realidad, y en el mejor de los casos,
sólo podríamos visualizar el hábito
externo de los
cristales, ¡si es que éstos están bien
formados!.Aunque aquí no vamos a responder a esta pregunta,
sí podemos adelantar que la respuesta nos la dará
el propio
comportamiento de los cristales cuando los iluminamos con la luz
especial que conocemos con el nombre de rayos X, pero eso
será objeto de otro capítulo.
En
cualquier caso,
esto
no acaba aquí y hay muchas más cosas que contar
...
Siguiente
capítulo: Redes directa y recíproca
Tabla de
contenido
