In X-ray diffraction the
scattering factor (ƒ) for an atom is roughly
proportional to the number of electrons that it possesses. However, for
wavelengths that approximate those for which the atom strongly absorbs
radiation, the scattering factor undergoes a change due to anomalous
dispersion. This effect not only affects the magnitude of the factor
but also imparts a phase shift in the elastic collision of the X
photon.
The scattering factor can therefore best be described as a complex
number:

The intensities of reflexions I(h,k,l) and I(-h,-k,-l) are equal either if the crystal structure is centrosymmetric or if there is no anomalous dispersion, but differ otherwise.

Friedel's Law is fulfilled in centrosymmetric crystals or in absence of anomalous dispersion.
In the absence of anomalous dispersion in non-centrosymmetric crystals, the structure factors for reflexions such as F(h,k,l) and F(-h,-k,-l) appear as reflected across the real axis of an Argand diagram (figure below). That is, their corresponding diffracted intensities, I(h,k,l) and I(-h,-k,-l), are equal and therefore they fulfill the Friedel’s Law.

Friedel's Law is fulfilled in the absence of anomalous dispersion.
However, the electric field associated to an incident photon can exert a force on electrons, affecting their natural oscillation frequency of vibration (its resonance frequency or resonant frequency) producing an energy transition, which is responsible of the anomalous dispersion effect. In mechanical systems this type of resonance effect may cause violent swaying motions and even catastrophic failure in improperly constructed structures including bridges, buildings and airplanes, a phenomenon known as resonance disaster.
Thus, anomalous dispersion occurs in non-centrosymmetric crystals when the incident radiation has sufficient energy to be absorbed by an atom in the structure, promoting an electronic transition, from a lower energy level to an upper one. The figure on the left shows the case of the Selenium atom. ∆E is near 8 KeV for most heavy and some light elements, so anomalous signal can be measured on a home X-ray source with Cu Kα radiation (8 KeV, λ=1.54 Å). At a synchrotron, the energy of the incident radiation can be tuned to match accurately ∆E (λ=0.98 Å for Se).

If the incident radiation has sufficient energy to be absorbed by an atom, electronic transitions can occur.
(Diagram reproduced by courtesy of Michael R. Sawaya)
When these electron transitions occur the corresponding atomic scattering factor (f) behaves as a complex number, appearing with two correction terms, a real number (f ' ) and an imaginary one (f ''). Its total value is dependent on the frequency of the incident photon ν, where νB is the electron natural frequency of oscillation (Bohr frequency) and g is the oscillator strength for the corresponding electron transition.

In order to interpret how this correction factors modify the scattering factor, one has to take into account that the real component (f ' ) is 180 degrees out of phase with the normally scattered radiation, and that the imaginary component (f '' ) is 90 degrees out of phase with the normally scattered radiation. Therefore, the existence of anomalous dispersion always implies that the total scattering radiation diminishes, what on the other hand can also be understood because a fraction of the scattered radiation is absorbed to produce the electronic transition.

The real component (f ') is 180 degrees out of phase with the normally scattered radiation. The imaginary component (f '') is 90 degrees out of phase.
Consequently, in a crystal where all atoms are under conditions of anomalous dispersion (i.e., all their atoms are heavy atoms: "H"), the Friedel’s law is broken due to a change in the phases of their scattered waves, although their intensities are still equal:

In a crystal with all atoms being under anomalous dispersion, the Friedel's Law is broken due to phase differences only.
However, this situation changes when some atoms in the crystal (lighter atoms: "L") do not show anomalous dispersion. In these circumstances, which are the normal ones in crystals, that is, when both normal and anomalous dispersors are present, the Friedel’s Law is totally broken. Reflexions of type (h,k,l) and (-h,-k,-l) are not only different in their phases. There is also an observable difference between the moduli of their structure factors |F(h,k,l)| and |F(-h,-k,-l)|, that is between their corresponding intensities, I(h,k,l) and I(-h,-k,-l).
This weak signals, ΔI , typically low (<3%) and not always easy to measure, can be used to solve the phase problem (mainly using MAD), and also to determine the absolute configuration of molecules.
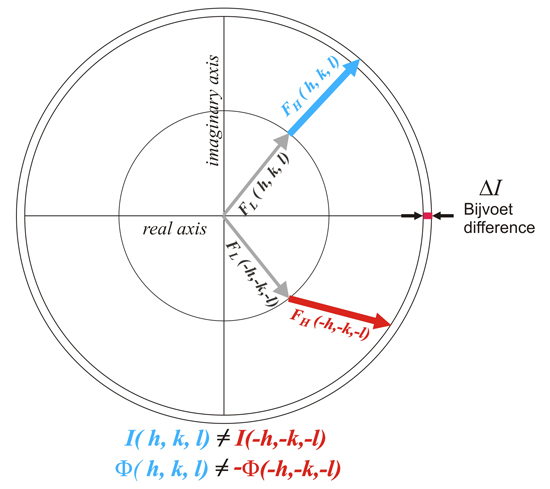
When both normal and anomalous dispersors are present, Friedel’s Law is totally broken.

The intensities of reflexions I(h,k,l) and I(-h,-k,-l) are equal either if the crystal structure is centrosymmetric or if there is no anomalous dispersion, but differ otherwise.

Friedel's Law is fulfilled in centrosymmetric crystals or in absence of anomalous dispersion.
In the absence of anomalous dispersion in non-centrosymmetric crystals, the structure factors for reflexions such as F(h,k,l) and F(-h,-k,-l) appear as reflected across the real axis of an Argand diagram (figure below). That is, their corresponding diffracted intensities, I(h,k,l) and I(-h,-k,-l), are equal and therefore they fulfill the Friedel’s Law.

Friedel's Law is fulfilled in the absence of anomalous dispersion.
However, the electric field associated to an incident photon can exert a force on electrons, affecting their natural oscillation frequency of vibration (its resonance frequency or resonant frequency) producing an energy transition, which is responsible of the anomalous dispersion effect. In mechanical systems this type of resonance effect may cause violent swaying motions and even catastrophic failure in improperly constructed structures including bridges, buildings and airplanes, a phenomenon known as resonance disaster.
Thus, anomalous dispersion occurs in non-centrosymmetric crystals when the incident radiation has sufficient energy to be absorbed by an atom in the structure, promoting an electronic transition, from a lower energy level to an upper one. The figure on the left shows the case of the Selenium atom. ∆E is near 8 KeV for most heavy and some light elements, so anomalous signal can be measured on a home X-ray source with Cu Kα radiation (8 KeV, λ=1.54 Å). At a synchrotron, the energy of the incident radiation can be tuned to match accurately ∆E (λ=0.98 Å for Se).

If the incident radiation has sufficient energy to be absorbed by an atom, electronic transitions can occur.
(Diagram reproduced by courtesy of Michael R. Sawaya)
When these electron transitions occur the corresponding atomic scattering factor (f) behaves as a complex number, appearing with two correction terms, a real number (f ' ) and an imaginary one (f ''). Its total value is dependent on the frequency of the incident photon ν, where νB is the electron natural frequency of oscillation (Bohr frequency) and g is the oscillator strength for the corresponding electron transition.

If
anomalous dispersion occurs, the
atomic scattering factor (f)
behaves as a complex number.
(Diagrams and mathematical expressions reproduced by courtesy of Michael R. Sawaya)
(Diagrams and mathematical expressions reproduced by courtesy of Michael R. Sawaya)
In order to interpret how this correction factors modify the scattering factor, one has to take into account that the real component (f ' ) is 180 degrees out of phase with the normally scattered radiation, and that the imaginary component (f '' ) is 90 degrees out of phase with the normally scattered radiation. Therefore, the existence of anomalous dispersion always implies that the total scattering radiation diminishes, what on the other hand can also be understood because a fraction of the scattered radiation is absorbed to produce the electronic transition.

The real component (f ') is 180 degrees out of phase with the normally scattered radiation. The imaginary component (f '') is 90 degrees out of phase.
Consequently, in a crystal where all atoms are under conditions of anomalous dispersion (i.e., all their atoms are heavy atoms: "H"), the Friedel’s law is broken due to a change in the phases of their scattered waves, although their intensities are still equal:
IH(h,k,l) = IH(-h,-k,-l)
That is, |FH(h,k,l)|
= |FH(-h,-k,-l)|
as it can be seen in the figure
below:
In a crystal with all atoms being under anomalous dispersion, the Friedel's Law is broken due to phase differences only.
However, this situation changes when some atoms in the crystal (lighter atoms: "L") do not show anomalous dispersion. In these circumstances, which are the normal ones in crystals, that is, when both normal and anomalous dispersors are present, the Friedel’s Law is totally broken. Reflexions of type (h,k,l) and (-h,-k,-l) are not only different in their phases. There is also an observable difference between the moduli of their structure factors |F(h,k,l)| and |F(-h,-k,-l)|, that is between their corresponding intensities, I(h,k,l) and I(-h,-k,-l).
This weak signals, ΔI , typically low (<3%) and not always easy to measure, can be used to solve the phase problem (mainly using MAD), and also to determine the absolute configuration of molecules.

When both normal and anomalous dispersors are present, Friedel’s Law is totally broken.
