INTRODUCTION
 The impossibility
of measuring the relative phases
among the diffracted beams, Φ(hkl), makes unfeasible a direct calculation of
the
electron density function
(Formula 1, below), which would provide us the atomic positions within
the unit cell. This was remedied only after 1934
when Arthur
Lindo Patterson
(1902-1966) introduced his brilliant idea, thereby obtaining the first solution
to the phase problem..., as he demonstrated in
his article entitled A
Fourier Series Method for the Determination of the Components of
Interatomic Distances in Crystals, A.L. Patterson (1934) Phys. Rev.,
46, 372-376. If you
have no access to this article in Phys.Rev., you may get a
photograph of its pages (except the last one), as provided by
the University
of Illinois.
The impossibility
of measuring the relative phases
among the diffracted beams, Φ(hkl), makes unfeasible a direct calculation of
the
electron density function
(Formula 1, below), which would provide us the atomic positions within
the unit cell. This was remedied only after 1934
when Arthur
Lindo Patterson
(1902-1966) introduced his brilliant idea, thereby obtaining the first solution
to the phase problem..., as he demonstrated in
his article entitled A
Fourier Series Method for the Determination of the Components of
Interatomic Distances in Crystals, A.L. Patterson (1934) Phys. Rev.,
46, 372-376. If you
have no access to this article in Phys.Rev., you may get a
photograph of its pages (except the last one), as provided by
the University
of Illinois.
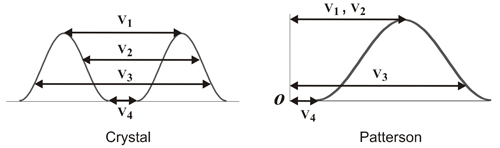
Patterson derived his function, P(uvw), (Formula 2 below) by introducing some modifications into the electron density function, so that the structure factors, represented by their amplitudes, [F(hkl)] and phases Φ(hkl), are replaced by the squared amplitudes whose values are proportional to the diffracted intensities (Formula 3 below). Therefore, the Patterson function can be directly calculated from the experimental data obtained in the diffraction experiment. However, the issue is to obtain the atomic coordinates from this new function...


Formula 2. The Patterson Function

Formula 3. The relationship between structure factor amplitude and intensity. K is a scale factor, A is the absorption factor, L is the Lorentz factor, and p represents the polarization factor
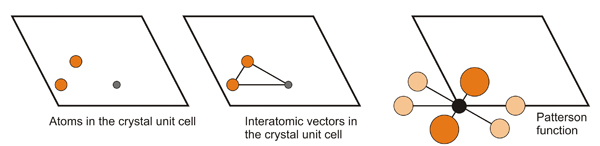
The information provided by the maxima of the Patterson Function corresponds to a map of position vectors (relative positions) between each pair of atoms in the structure. The value of the function at these maxima is proportional to the product of the implied atomic numbers, which provides a clear advantage for detecting vectors between "heavy" atoms, ie atoms with a large number of electrons.
If the crystal space (where the atoms are) is defined by the value of the ρ function at every point in the unit cell given by the coordinates (x, y, z), the Patterson space (also periodic and defined by a unit cell identical to the crystal unit cell) is defined by the generic coordinates <u, v, w>, in such a way that any pair of atoms in the crystal, located at (x1, y1, z1) and (x2, y2, z2), will be shown in the Patterson map by a maximum with coordinates:
 The impossibility
of measuring the relative phases
among the diffracted beams, Φ(hkl), makes unfeasible a direct calculation of
the
electron density function
(Formula 1, below), which would provide us the atomic positions within
the unit cell. This was remedied only after 1934
when Arthur
Lindo Patterson
(1902-1966) introduced his brilliant idea, thereby obtaining the first solution
to the phase problem..., as he demonstrated in
his article entitled A
Fourier Series Method for the Determination of the Components of
Interatomic Distances in Crystals, A.L. Patterson (1934) Phys. Rev.,
46, 372-376. If you
have no access to this article in Phys.Rev., you may get a
photograph of its pages (except the last one), as provided by
the University
of Illinois.
The impossibility
of measuring the relative phases
among the diffracted beams, Φ(hkl), makes unfeasible a direct calculation of
the
electron density function
(Formula 1, below), which would provide us the atomic positions within
the unit cell. This was remedied only after 1934
when Arthur
Lindo Patterson
(1902-1966) introduced his brilliant idea, thereby obtaining the first solution
to the phase problem..., as he demonstrated in
his article entitled A
Fourier Series Method for the Determination of the Components of
Interatomic Distances in Crystals, A.L. Patterson (1934) Phys. Rev.,
46, 372-376. If you
have no access to this article in Phys.Rev., you may get a
photograph of its pages (except the last one), as provided by
the University
of Illinois.Patterson derived his function, P(uvw), (Formula 2 below) by introducing some modifications into the electron density function, so that the structure factors, represented by their amplitudes, [F(hkl)] and phases Φ(hkl), are replaced by the squared amplitudes whose values are proportional to the diffracted intensities (Formula 3 below). Therefore, the Patterson function can be directly calculated from the experimental data obtained in the diffraction experiment. However, the issue is to obtain the atomic coordinates from this new function...

Formula
1. Electron
density function

Formula 2. The Patterson Function

Formula 3. The relationship between structure factor amplitude and intensity. K is a scale factor, A is the absorption factor, L is the Lorentz factor, and p represents the polarization factor
The information provided by the maxima of the Patterson Function corresponds to a map of position vectors (relative positions) between each pair of atoms in the structure. The value of the function at these maxima is proportional to the product of the implied atomic numbers, which provides a clear advantage for detecting vectors between "heavy" atoms, ie atoms with a large number of electrons.
If the crystal space (where the atoms are) is defined by the value of the ρ function at every point in the unit cell given by the coordinates (x, y, z), the Patterson space (also periodic and defined by a unit cell identical to the crystal unit cell) is defined by the generic coordinates <u, v, w>, in such a way that any pair of atoms in the crystal, located at (x1, y1, z1) and (x2, y2, z2), will be shown in the Patterson map by a maximum with coordinates:
u
= x1 - x2 ;
v=
y1 - y2 ;
w
= z1 - z2